menu
search
知识点
登录
登录
第四周
查看历史成绩
2025-09-27
填空题
1.
因式分解: $4(a-c)^2-2(c-a)^2$
错误
正确
填空题
2.
因式分解: $4(x-y)^2+4(x-y)+1$
错误
正确
填空题
3.
因式分解: $4x^4-64$
错误
正确
填空题
4.
因式分解: $3a(a+b)^2-27ab^2$
错误
正确
填空题
5.
因式分解: $3x^3-12x^2y+12xy^2$
错误
正确
填空题
6.
因式分解: $(x^2-3x)^2-2(x^2-3x+4)$
错误
正确
填空题
7.
计算: $\frac{2a-3}{5a} \cdot \frac{10b}{6ab-9b}$
错误
正确
填空题
8.
计算: $\frac{2a-3}{5a^2} \div \frac{6a-9}{15a}$
错误
正确
计算题
9.
计算: $\frac{x^2-6x+5}{x^2-1} \div \frac{x^2+6x-7}{x^2+8x+7}$
错误
正确
解答题
10.
观察下列分解因式的过程: $a^2+2ab-3b^2$ 解: 原式 = $a^2+2ab+b^2-b^2-3b^2$ = $(a^2+2ab+b^2) - 4b^2$ = $(a+b)^2-4b^2$ = $(a+b+2b)(a+b-2b)$ = $(a+3b)(a-b)$ 像这种通过增减项把多项式转化成完全平方形式的方法称为配方法。 1) 请你运用上述配方法分解因式: $a^2+4ab-5b^2$ 2) 代数式 $a^2+2a+b^2-6b+12$ 是否存在最小值?如果存在,请求出当a,b分别是多少时,此代数式存在最小值,最小值是多少?如果不存在,请说明理由。
错误
正确
填空题
11.
因式分解 $(x-1)(x+2)(x-3)(x-6)+56$
错误
正确
填空题
12.
因式分解: $(x+1)(x+2)(x+3)(x+4)+x(x+5)$
错误
正确
填空题
13.
因式分解: $(x^2-5x+6)(x^2-10x+24) - 30x^2$
错误
正确
填空题
14.
因式分解: $(x^4+x^2+7)(x^4+x^2-12)+78$
错误
正确
填空题
15.
化简: $-(x^3-x+1)\cdot(-x)^2 - (-x)^3(x^2-1)$
错误
正确
填空题
16.
计算 $(-\frac12x-2y)(\frac12x-2y)$
错误
正确
填空题
17.
计算: $(2a-3b)(b+2a)$
错误
正确
填空题
18.
化简求值 $(-2x)^2 + (2x-5y)(2x+3y) - 3y(4x-5y)$, 其中 x=2, y=-1
错误
正确
填空题
19.
计算: $(-2)^5+2\times(-2)^4$
错误
正确
填空题
20.
解方程: $(3x^2-1)(x+3)-(2x-1)(x+1) = x(3x^2+7x)+4$
错误
正确
填空题
21.
计算: $\frac{y}{4x^2-y^2} - \frac{2x}{4x^2-y^2}$
错误
正确
计算题
22.
计算: $\frac2{x-1}+\frac{x-1}{1-x}$
错误
正确
解答题
23.
已知一个最简分式乘以 $\frac{x^2-y^2}{x^2+2xy+y^2}$ 的积是 $\frac{x-y}{(x+y)^3}$, 求原来这个最简分式
错误
正确
计算题
24.
计算: $\frac{3x}{2-x} + \frac{6}{x-2}$
错误
正确
计算题
25.
计算: $\frac{x^2}{x^2-16}-\frac{2}{x-4}$
错误
正确
填空题
26.
计算: $\frac{x^3-3x^2}{x^2-1}\cdot\frac{x+1}{x-3}-\frac{x}{x-1}$
错误
正确
填空题
27.
计算: $\frac{x^2-2xy}{x^2-3xy+2y^2}-\frac{xy+y^2}{x^2-y^2}$
错误
正确
计算题
28.
计算: $\frac{a-b}{a^2-b^2}-\frac2{a+b}$
错误
正确
计算题
29.
计算: $\frac3{2m-n} - \frac{2m-n}{(2m-n)^2}$
错误
正确
计算题
30.
计算: $\frac{x-1}{x-2}\cdot(\frac{x^2-4}{x^2-x}-\frac{x^2-2x}{x^2-1})$
错误
正确
填空题
31.
计算: $-a^4\cdot(-a^2)^3$
错误
正确
选择题
32.
下列各式中能用完全平方式因式分解的有 ( ) $x^2-10x+25$, $4a^2+4a-1$, $x^2-2x+1$, $-m^2+m-\frac14$, $4x^4-x^2+\frac14$ A. 1个 B. 2个 C. 3个 D. 4个
错误
正确
填空题
33.
如果代数式 $A=-3m^2-4m+1, B=-4m-5m^2$ , 那么无论m取何值,代数式 A 与 B 的取值大小关系一定是 ( ) A. A\<B B. A\>B C. A=B D. 都有可能
错误
正确
填空题
34.
因式分解: $x^2+5xy-6y^2$
错误
正确
填空题
35.
已知 $a-b=-1, b+c=-3$, 则 $a^2-bc+ac-ab$ 的值为: ___________
错误
正确
填空题
36.
现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片( $\frac12a<b<a$ )如图1,取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图 2,再重新用三张小正方形卡片放入“大正方形”内拼成的图案如图3,已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab-15,则小正方形卡片的面积是 __________________ 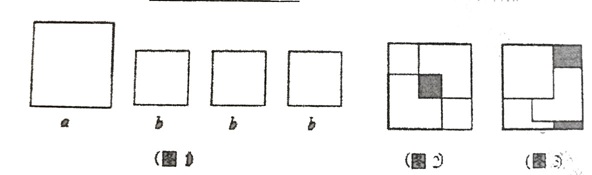
错误
正确
填空题
37.
已知 $x\neq y, x^2-x=7, y^2-y=7$, 求 $x^3+y^3+x^2y+xy^2$ 的值
错误
正确
填空题
38.
在整式乘法的学习中,我们采用了构造几何图形的方法研究代数式的恒等变形问题,借助直观、形象的几何图形,加深对整式乘法的认识和理解,感悟代数与几何的内在联系,这种方法同样适用于因式分解的学习. 如图1,现有边长分别为a,b的正方形 I 号和 II 号,以及长为a,宽为b的长方形Ⅲ号卡片,我们可以选取适量的卡片拼接成几何图形(卡片间不重叠无缝隙) 解答下列问题: 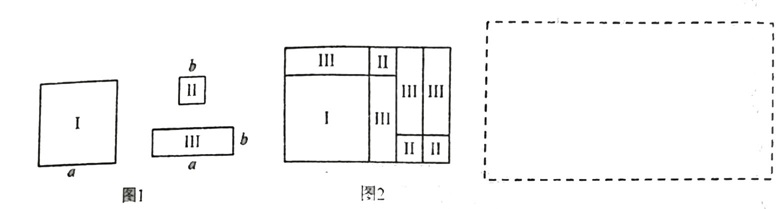 1) 图2的长方形是由图1中1张 I 号、3张 II 号和4张 III 号卡片拼接而成,则这个几何图形表示的关于因式分解的等式是____________________________; 2) 若想用几何图形验证 $2a^2+3ab+b^2=(a+b)(2a+b) $,请你利用图1中的若干张卡片,画出相应的拼接图形(画在上图方框内); 3) 设a=3,b=1,1号、Ⅱ号和 III 号每种卡片各有9张,从其中取若干张卡片(每种卡片至少取1张),若把取出的这些卡片拼成一个正方形,当所拼正方形的边长最大时,则所用卡片的最少数量为 _______ 张
错误
正确
解答题
39.
图(1)是一块智慧黑板的平面示意图,由①、②、③、④四块长方形小黑板组成,四块小黑板的长和宽如图所示(其中a<6),②和③号黑板分别可以向左、向右水平移动,移动后就可以看到黑板后的电子屏幕  (1)将②号黑板向左水平移动,使EF与AB重合,③号黑板向右水平移动,使MN与DC重合,此时电子屏幕全部呈现,没有黑板遮挡,如图(2)所示.求电子屏幕的面积;(用含a、b的代数式表示) (2)将②号黑板向左水平移动的距离为 $\frac14a$,将③号黑板水平向右水平移动一定的距离,此时被黑板遮挡住的电子屏幕的面积为 $\frac{a^2+2ab+b^2}{4}$ ,求③号黑板向右水平移动的距离.(用含a、b的代数式表示)
错误
正确
填空题
40.
如果计算 $(x^2+x+1)(x^2-3x+a)(2x-1)$ 所得多项式的一次项系数为0,那么 a = ______ 如果 $x^2-3x+1$ 是 $x^4+ax^2+bx+2$ 的一个因式,求 $2a+b$ 的值。
错误
正确
提交判题
沪ICP备2024105194号
沪公网安备31011702890224号
毛爸作品