menu
search
知识点
登录
登录
第5周
查看历史成绩
2025-11-24
选择题
1.
如果 a+b=3, 则代数式 $a^2-b^2+6b$ 的值为 ______ A. 3 B. 6 C. 9 D. 12
错误
正确
填空题
2.
因式分解: $3x^2-6x+3$
错误
正确
解答题
3.
阅读材料 小明遇到这样一个问题:求计算(x+2)(2x+3)(3x+4)所得多项式的一次项系数. 小明想通过计算(x+2)(2x+3)(3x+4)所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法. 他决定从简单情况开始,先找(x+2)(2x+3)所得多项式中的一次项系数.通过观察发现:  也就是说,只需用x+2中的一次项系数1乘以2x+3中的常数项3,再用x+2中的常数项2乘以2x+3中的一次项系数2,两个积相加1x3+2x2=7即可得到一次项系数. 延续上面的方法,求计算(x+2)(2x+3)(3x+4)所得多项式的一次项系数.可以先用x+2的一次项系数1,2x+3的常数项3,3x+4的常数项4,相乘得到12;再用2x+3的一次项系数2,x+2的常数项2,3x+4的常数项4,相乘得到16;然后用3x+4的一次项系数3,x+2的常数项2,2x+3的常数项 3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题: - (1)计算(2x+1)(3x+2)所得多项式的一次项系数为______ - (2)计算(x+1)(3x+2)(4x-3)所得多项式的一次项系数为_______ - (3)如果计算 $(x^2+x+1)(x^2-3x+a)(2x-1)$ 所得多项式的一次项系数为0那么a=____ - (4)如果 $x^2-3x+1$ 是 $x^4+ax^2+bx+2$ 的一个因式,求2a+b的值
错误
正确
填空题
4.
$(-a^3)^{-2}\cdot(-a^2)^3$ = ____________
错误
正确
填空题
5.
已知 a - b = 3, ab = 2, 则 $a^4b^2-2a^3b^3+a^2b^4$ 的值是______________
错误
正确
计算题
6.
$\frac{2x}{9-x^2}+\frac1{x-3}+\frac2{x^2+6x+9}$
错误
正确
填空题
7.
$\frac{3x-2}{x^2-x-2}+(1-\frac1{x+1})\div(1+\frac1{x-1})$
错误
正确
填空题
8.
$\frac{a^2}{a^2-4}+\frac4{a+2-a^2}+\frac{4a-4}{a^4-5a^2+4}$
错误
正确
填空题
9.
$\frac{x+3y}{x^2+xy}+\frac{y-x}{xy+y^2}$
错误
正确
填空题
10.
$\frac1{x+1}\cdot(\frac{x-3}{x^2+6x+9}+\frac2{3+x})-\frac{x}{x^2-9}$
错误
正确
填空题
11.
$(x-1+\frac2{x-4})\div(x-3-\frac2{x-4})$
错误
正确
填空题
12.
$3-(\frac4{x-2}+1)(\frac4x-4+x)\div(1-\frac4{x^2})$
错误
正确
填空题
13.
若x=1是方程 $\frac{x+2}{x-1}+\frac{x+3}{x-2}=\frac{m}{(x-1)(x-2)}$ 的增根,则 m=_______
错误
正确
填空题
14.
若方程 $\frac{3}{x+3}=\frac{2}{x+k}$ 的解为负数,则k的取值范围是 _____________
错误
正确
填空题
15.
若分式方程 $\frac{x+a}{x-1}=a$ 无解,则a的值为___________
错误
正确
解方程
16.
$\frac{x-2}{2x+2}+\frac{2x+2}{x-2} = 2$
错误
正确
填空题
17.
$\frac{x+1}{x-1} - \frac{4}{x^2-1}=1$
错误
正确
解方程
18.
$\frac{1-3x}{1+3x}+\frac{3x+1}{3x-1} = \frac{12}{1-9x^2}$
错误
正确
解方程
19.
$\frac{1}{x-7}+\frac{1}{x-1}=\frac{1}{x-6}+\frac{1}{x-2}$
错误
正确
填空题
20.
如图, $\triangle$ DEF 是直角三角形 ABC 沿BC平移得到的,如果AB=7, BE=2,DH=1,则图中阴影部分的面积是 ___________ 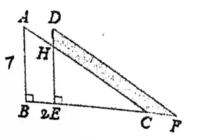
错误
正确
解答题
21.
如图, $\triangle ABC$ 经过一次平移到 $\triangle DFE$ 的位置,请回答下列问题: (1) 点 C 的对应点是点 _________ , $\angle D$ = __________, BC = _______ 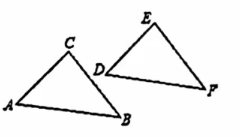 (2) 连接 CE,那么平移的方向就是 ___________ 的方向,平移的距离就是线段 ___________ 的长度。 (3) 连接 AD、BF、BE,与线段CE相等的线段有_____________
错误
正确
填空题
22.
如图所示,长方形 ABCD 中,对角线 AC,BD交于点O。DE平行于AC,CE平行于BD,那么三角形EDC可以看成什么三角形平移得到的,指出平移方向,并指出平移距离。 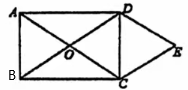
错误
正确
填空题
23.
如图,将三角形 ABC向右平移4格,再向下平移3格后的图形为三角形 $A_1B_1C_1$. 如果线段 AB的中点是点D,请画出它的对应点的位置。 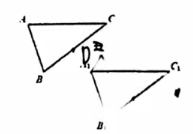
错误
正确
填空题
24.
如图所示,在长为 50 米,宽为 25 米的草坪上修了一条宽恒为1米宽的弯曲小路,则余下草坪的面积是 ___________ 平方米。 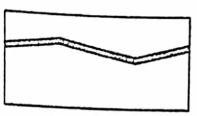
错误
正确
提交判题
沪ICP备2024105194号
沪公网安备31011702890224号
毛爸作品